Тип 0 № 3890 
Классификатор: Оптика. Освещенность
i
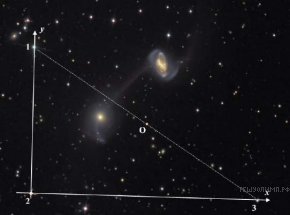(«Галактическая навигация») Обитатели системы О часто совершают полеты в плоскости (xy), в которой система декартовых координат связана с тремя удачно расположенными в этой плоскости яркими объектами (обозначенными на рисунке цифрами 1,2 и 3).
Расстояние между 1 и 2 
кпс (парсек (пс) — астрономическая единица длины 
а между 2 и 3 
кпс, угол между осями x и y прямой, а система О лежит точно между 1 и 3. Для ориентации в данной плоскости корабли оснащены телескопами, постоянно нацеленными на объекты 1, 2 и 3, свет от которых фокусируется на фотодатчиках. Датчики отрегулированы так, что при нахождении корабля рядом с системой О их токи одинаковы и равны 
мА (ток датчика пропорционален мощности поступающего светового сигнала). Определите координаты корабля в этой системе координат, если токи датчиков равны 
мА, 
мА и 
мА. На каком расстоянии от системы О находится в этот момент корабль? Поглощением света в межзвездной среде можно пренебречь.
Решение. Добавим третью координатную ось (z), перпендикулярную нашей плоскости. Пусть x, y и z — координаты корабля (в кпс). Тогда расстояния от корабля до ярких объектов 1, 2, 3 удовлетворяют соотношениям:
По условию поглощением света в межзвездной среде можно пренебречь. Тогда поток энергии излучения (энергия, проходящая в единицу времени через единицу площади волнового фронта), распределяющейся на некотором расстоянии r от источника по поверхности сферы площадью 
Следовательно, мощность излучения, попадающего в «приемное окно» датчика, обратно пропорционально квадрату расстояния до соответствующего объекта. При нахождении корабля радом с системой О все три объекта находятся от него на одинаковом расстоянии
Таким образом, ток датчика c номером i равен
Следовательно,
и
Вычитая эти соотношения, находим, что
Аналогично комбинируя выражение
с выражением для 
получим
Теперь мы обнаруживаем, что наш корабль вылетел из «привычной» плоскости, так как
Так как z входит в уравнения только в форме квадрата, то могут быть два возможных значения 
Ясно, что координаты системы О равны 
и 
Поэтому расстояние от корабля до системы О равно
Ответ: координаты корабля x = 65 кпс, y = 5 кпс и 
кпс, расстояние от корабля до системы О 
Спрятать критерииКритерии проверки:| Действия | Макс. балл. |
|---|
| Записаны правильные выражения для расстояний до объектов через искомые координаты корабля | 3 · 1 = 3 |
| Доказано, что ток мощность принимаемого датчиком излучения обратно пропорциональна квадрату расстояния до соответствующего объекта | 4 |
| Записаны правильные уравнения, связывающие координаты корабля с отношениями токов фотодатчиков | 3 · 2 = 6 |
| Правильно найдена координата x = 65 кпс (с ошибкой не более 0,3 кпс) | 2* |
| Правильно найдена координата y = 5 кпс (с ошибкой не более 0,2 кпс) | 2* |
| Обнаружено, что корабль покинул плоскость (xy) | 2* |
Правильно найдена координата  (с ошибкой не более 0,3 кпс) | 2 · 1 = 2* |
Правильно найдено расстояние  (с ошибкой не более 0,5 кпс) | 1* |
| Всего | 22 |
(*) Допускается решение «в числах», без получения формул в общем виде.
Ответ: координаты корабля
x = 65 кпс,
y = 5 кпс и
кпс, расстояние от корабля до системы О
Классификатор: Оптика. Освещенность
