Тип 0 № 3065 

Классификатор: Механика. Закон сохранения энергии в конс. системах
i
Вопрос. Жесткий стержень движется в плоскости. В некоторый момент времени скорость одного из его концов равна 0,4 м/с и направлена вдоль стержня. В тот же момент времени скорость другого конца стержня равна 0,8 м/с. Под каким углом к стержню направлена эта скорость? Ответ объяснить.
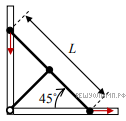
Задача. Вам необходимо изучить движение следующего механического устройства: три одинаковых массивных шарика прикреплены к концам и середине легкого жесткого стержня. Длина стержня L = 1,2 м. Крайние шарики могут без трения скользить по вертикальной и горизонтальной направляющим (см. рисунок). Средний шарик шарнирно соединен с легким жестким стержнем вдвое меньшей длины. Второй конец этого стержня прикреплен (также с помощью шарнира) к перекрестью направляющих. Изначально стержень располагают вдоль вертикальной направляющей и отпускают без начальной скорости. Трения нигде нет, крайние шарики не отрываются от направляющих и не застревают в них. По какой траектории будет двигаться средний шарик? Куда будет направлена его скорость в тот момент, когда длинный стержень будет проходить положение, в котором он составляет 45° с горизонтом? Найдите величину этой скорости. Ускорение свободного падения  м/с2.
м/с2.
Решение. Ответ: Так как длина «жесткого» стержня не должна изменяться, то проекции скоростей его точек на стержень должны быть одинаковы и поэтому равны 0,4 м/с. Такой должна быть и проекция скорости «другого конца», то есть проекция (катет прямоугольного треугольника, образованного вектором скорости, его проекцией и перпендикуляром к стержню) должна равняться половине самой скорости (гипотенузы). Значит, прилежащий угол для этого катета угол между скоростью и стержнем — равен 60°.
Решение задачи. Расстояние между средним шариком и перекрестьем направляющих все время остается постоянным (равным половине L). Поэтому ясно, что средний шарик движется по окружности радиуса 
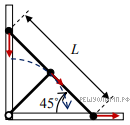 Его скорость в любой момент времени направлена по касательной к этой окружности, и в момент, когда длинный стержень будет проходить положение, в котором он составляет 45° с горизонтом, эта скорость будет направлена вдоль стержня. Пусть ее величина в этот момент равна υ. Так как длина стержня не должна изменяться, то проекции скоростей шариков на стержень должны быть одинаковы, поэтому скорости крайних шариков в этот момент одинаковы и равны
Его скорость в любой момент времени направлена по касательной к этой окружности, и в момент, когда длинный стержень будет проходить положение, в котором он составляет 45° с горизонтом, эта скорость будет направлена вдоль стержня. Пусть ее величина в этот момент равна υ. Так как длина стержня не должна изменяться, то проекции скоростей шариков на стержень должны быть одинаковы, поэтому скорости крайних шариков в этот момент одинаковы и равны  Следовательно, кинетическая энергия системы в этот момент времени
Следовательно, кинетическая энергия системы в этот момент времени

Так как эта энергия появилась из-за убыли потенциальной энергии верхнего и среднего шариков в поле тяжести Земли

то

и из этого соотношения находим, что

Ответ: средний шарик движется по окружности радиуса  в указанный момент времени его скорость направлена вниз вдоль длинного стержня, а ее величина
в указанный момент времени его скорость направлена вниз вдоль длинного стержня, а ее величина 
Спрятать критерииКритерии проверки:Максимальная оценка за вопрос — 5 технических баллов.
Максимальная оценка за задачу — 20 технических баллов.
Ответ: Так как длина «жесткого» стержня не должна изменяться, то проекции скоростей его точек на стержень должны быть одинаковы и поэтому равны 0,4 м/с. Такой должна быть и проекция скорости «другого конца», то есть проекция (катет прямоугольного треугольника, образованного вектором скорости, его проекцией и перпендикуляром к стержню) должна равняться половине самой скорости (гипотенузы). Значит, прилежащий угол для этого катета угол между скоростью и стержнем — равен 60°.
Решение задачи. Расстояние между средним шариком и перекрестьем направляющих все время остается постоянным (равным половине L). Поэтому ясно, что средний шарик движется по окружности радиуса 
 Его скорость в любой момент времени направлена по касательной к этой окружности, и в момент, когда длинный стержень будет проходить положение, в котором он составляет 45° с горизонтом, эта скорость будет направлена вдоль стержня. Пусть ее величина в этот момент равна υ. Так как длина стержня не должна изменяться, то проекции скоростей шариков на стержень должны быть одинаковы, поэтому скорости крайних шариков в этот момент одинаковы и равны
Его скорость в любой момент времени направлена по касательной к этой окружности, и в момент, когда длинный стержень будет проходить положение, в котором он составляет 45° с горизонтом, эта скорость будет направлена вдоль стержня. Пусть ее величина в этот момент равна υ. Так как длина стержня не должна изменяться, то проекции скоростей шариков на стержень должны быть одинаковы, поэтому скорости крайних шариков в этот момент одинаковы и равны  Следовательно, кинетическая энергия системы в этот момент времени
Следовательно, кинетическая энергия системы в этот момент времени

Так как эта энергия появилась из-за убыли потенциальной энергии верхнего и среднего шариков в поле тяжести Земли

то

и из этого соотношения находим, что

Ответ: средний шарик движется по окружности радиуса  в указанный момент времени его скорость направлена вниз вдоль длинного стержня, а ее величина
в указанный момент времени его скорость направлена вниз вдоль длинного стержня, а ее величина 
Классификатор: Механика. Закон сохранения энергии в конс. системах
м/с2.
Его скорость в любой момент времени направлена по касательной к этой окружности, и в момент, когда длинный стержень будет проходить положение, в котором он составляет 45° с горизонтом, эта скорость будет направлена вдоль стержня. Пусть ее величина в этот момент равна υ. Так как длина стержня не должна изменяться, то проекции скоростей шариков на стержень должны быть одинаковы, поэтому скорости крайних шариков в этот момент одинаковы и равны
Следовательно, кинетическая энергия системы в этот момент времени
в указанный момент времени его скорость направлена вниз вдоль длинного стержня, а ее величина



